Skip to content

Data Generation

In order to create process curves with a realistic behaviour of process drifts, driftbench synthesizes curves by solving nonlinear optimization problems. By defining a function \(f(w(t), t)\) and support points \(x\) and \(y\), we can solve for the internal parameters \(w(t)\) such that all the conditions given by the support points are satisfied. The schema is explained in the following section.

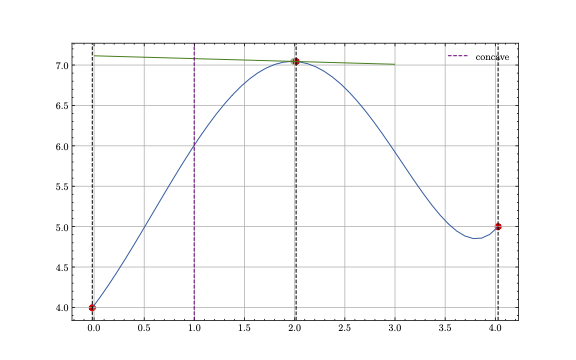
Example curve

Synthetization

In the first step, we need to define latent information which encodes the shape of the curves to synthesize. This is done by formulating such a spec in a yaml-file. For example, the following spec defines a polynomial of 7-th degree: 

example:
  N: 10000
  dimensions: 100
  x_scale: 0.2 
  y_scale: 0.2
  func: w[7]* x**7 + w[6]* x**6 + w[5]* x**5 +w[4]* x**4 + w[3] * x**3 + w[2] * x**2 + w[1] * x + w[0]
  w_init: np.zeros(8)
  latent_information:
    !LatentInformation
    x0: [0, 1, 3, 2, 4]
    y0: [0, 4, 7, 5, 0]
    x1: [1, 3]
    y1: [0, 0]
    x2: [1]
    y2: [0]
  drifts:
    !DriftSequence
      - !LinearDrift
        start: 1000
        end: 1100
        feature: y0     
        dimension: 2    
        m: 0.002
The root key defines the name of the dataset, in this case example. The other keys of this yaml structure are:

  • N: The number of curves to synthesize.
  • dimensions: The number of timesteps one curve consists of.
  • x_scale: The scale of a random gaussian noise which is applied to the x-latent information. If set to 0, no scale noise is applied.
  • y_scale: The scale of a random gaussian noise which is applied to the y-latent information. If set to 0, no scale noise is applied.
  • func: The function which defines the shape of a curve. The internal parameters are denoted as w, while the timesteps which are used to evaluate the curve are denoted as x.
  • w_init: The initial guess for the internal parameters. Must match the number of internal parameters defined in func.
  • latent_information: Contains a LatentInformation structure, which holds the latent information which defines the support points of the curves. The x_idenote the x-information for the i-th derivative of func, while the y_idenote the y-information respectively.
  • drifts: Contains a DriftSequence structure, which in turn holds a list of drifts, for example LinearDrift-structures. These drifts are applied in the specified manner on the latent information for each timestep defined as start as end within the N curves. The drift structure defines the feature and the dimension as well as internal parameters, like in this case the slope m.

After setting up such a specification, you can call the sample_curves-function, and retrieve the coefficients, respective latent information and curve for each timestep. 

coefficients, latent_information, curves = sample_curves(dataset["example"], measurement_scale=0.1)
By specifying a value for measurement_scale some gaussian noise with the specified scale is applied on each value for every curve. By default, \(5\%\) of the mean of the curves is used. If you want to omit the scale, set it to 0.0 explicitly.